Sound Theory
Human hearing beats the Fourier uncertainty principle
For the first time, physicists have found that humans can discriminate a sound's frequency (related to a note's pitch) and timing (whether a note comes before or after another note) more than 10 times better than the limit imposed by the Fourier uncertainty principle.
You can read about it here.
You can read about it here.
Hypersonic Sound
Here is a Powerpoint presentation on how it works. More information is available here.
| hypersonic_sound.pps | |
| File Size: | 367 kb |
| File Type: | pps |
Temperament
How we got Equal Temperament
We often take standards for granted. For example, an international standard tuning pitch of A=440Hz was not settled until 1939. After the middle ages local musicians could tune to the parish organ but these varied considerably in pitch (mainly due to climatic differences between the north and south of Europe). The problem became substantial when musicians started to travel throughout Europe, and lasted over 400 years!
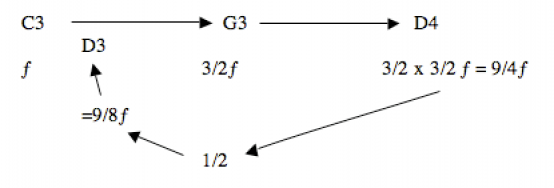
The history of the evolution of temperament is even longer (and more winding). Pythagoras (560-480BC), with his Greek sense of order, set out to find the pattern for a natural musical scale using nice ratios such as 3:2. eg:
If we carry on with our "circle of 5ths" we do derive all the notes of the major scale.
x3/2 x1/2
C3 = ƒ G3= 3/2ƒ D4= 9/4ƒ
D2 = 9/8ƒ A2= 27/16ƒ
F3 = 2ƒ(2/3) = 4/3ƒ
(Major Pentatonic Scale)
x3/2 x1/2
A3 = 27/16 E4= 81/32ƒ
E3 = 81/64ƒ B3= 243/128ƒ
x3/2 x1/2
C3 = ƒ G3= 3/2ƒ D4= 9/4ƒ
D2 = 9/8ƒ A2= 27/16ƒ
F3 = 2ƒ(2/3) = 4/3ƒ
(Major Pentatonic Scale)
x3/2 x1/2
A3 = 27/16 E4= 81/32ƒ
E3 = 81/64ƒ B3= 243/128ƒ
9/8 is the Pythagorean Whole tone ratio.
Multiplying by 1 x (9/8)6 =(B1#)/C2 = 2.0272865/2 = 1.0136432
Or to put it another way the ratio is 531441:524288 = 23.46 cents.
This "error" could not be resolved by Pythagoras , and came to be known as the Pythagorean comma.The only cure was to not deviate too far from the root note of the scale.
But there was worse to come - not only did the tuning not agree with the 2:1 ratio for the octave, but it affected intervals within the octave. This meant that it was difficult for some intervals to sound right when playing in a certain key, and impossible if there was any key change. For fixed pitch instruments, such as keyboards, this was starting to be a big problem.
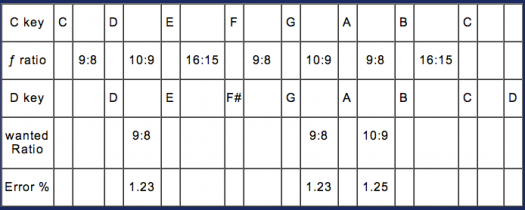
Pythagorean tuning ratios
Multiplying by 1 x (9/8)6 =(B1#)/C2 = 2.0272865/2 = 1.0136432
Or to put it another way the ratio is 531441:524288 = 23.46 cents.
This "error" could not be resolved by Pythagoras , and came to be known as the Pythagorean comma.The only cure was to not deviate too far from the root note of the scale.
But there was worse to come - not only did the tuning not agree with the 2:1 ratio for the octave, but it affected intervals within the octave. This meant that it was difficult for some intervals to sound right when playing in a certain key, and impossible if there was any key change. For fixed pitch instruments, such as keyboards, this was starting to be a big problem.
Pythagorean tuning ratios
So great was this problem that the best musical minds wrestled with it for centuries, trying to devise a universal tuning system that would keep things in tune regardless of which notes were played together. Early attempts were Just tuning ( a modified Pythagorean temperament – same for 4ths, 5ths and octaves. Most intervals are simpler ratios. Only good for the key it is tuned to), and Meantone (the 5th is flattened slightly. The 2nd degree of the scale was put exactly halfway between the tonic and the third).
Equal Temperament
This tuning puzzle was finally solved by non other than J S Bach. When he published The Well Tempered Clavier it became clear he had solved the problem as it contained 24 pieces of music for the keyboard, each in a different key (12 major, 12 minor). To enable playing several pieces without retuning the instrument meant that clever old Bach had indeed cracked the code (some musical historians pick up on a minor difference between Bach's "well" temperament and modern equal temperament - don't loose any sleep over it).
Equal temperament, as the name suggests, divides the semitones into 12 equal steps between the octave. Mathematically speaking this ratio is 1:2^(1/12). In other words each semitone has a step of the twelfth root of 2, which is:
1.05946309 (to eight decimal places).
Not exactly a nice Pythagorean type number! In fact, widespread adoption of equal temperament was not possible until the industrial revolution, when precision engineering became available.
For a comparison chart of Just, Pythagorean, and Equal Temperament ratios click the arrow.
For all its universal appeal, Equal Temperament is not a perfect answer. Some intervals are less in tune than they would be in the Pythagorean system (the major 3rd in particular). Listen to these examples to hear the difference:
Equal Temperament
This tuning puzzle was finally solved by non other than J S Bach. When he published The Well Tempered Clavier it became clear he had solved the problem as it contained 24 pieces of music for the keyboard, each in a different key (12 major, 12 minor). To enable playing several pieces without retuning the instrument meant that clever old Bach had indeed cracked the code (some musical historians pick up on a minor difference between Bach's "well" temperament and modern equal temperament - don't loose any sleep over it).
Equal temperament, as the name suggests, divides the semitones into 12 equal steps between the octave. Mathematically speaking this ratio is 1:2^(1/12). In other words each semitone has a step of the twelfth root of 2, which is:
1.05946309 (to eight decimal places).
Not exactly a nice Pythagorean type number! In fact, widespread adoption of equal temperament was not possible until the industrial revolution, when precision engineering became available.
For a comparison chart of Just, Pythagorean, and Equal Temperament ratios click the arrow.
For all its universal appeal, Equal Temperament is not a perfect answer. Some intervals are less in tune than they would be in the Pythagorean system (the major 3rd in particular). Listen to these examples to hear the difference:
| et.mid | |
| File Size: | 0 kb |
| File Type: | mid |
| meantone.mp3 | |
| File Size: | 440 kb |
| File Type: | mp3 |
| pythagorian.mp3 | |
| File Size: | 440 kb |
| File Type: | mp3 |
Here are the differences (in Cents) from equal temperament:
Hermode Tuning
Hermode tuning is a system which dynamically allocates the pitches of notes according to the harmonic context of the music. The idea is simple enough, but requires a complex set of rules according to what sequence of intervals are present in the chord progression of the piece (this is what vocalists can naturally do when singing a capella). This meant that it is only recently that a commercially viable solution has been possible (due to the computing power required). Hermode tuning is available in Logic Audio Pro. For more information visit the website www.hermode.com
Alternative Temperaments
Alpha, Beta, Gamma
Wendy (nee Walter) Carlos has been active in exploring experimental tunings. Of particular interest are her alpha, beta, and gamma scales. These split certain intervals into equal steps, which results in a strange sense of in-tuneness and out-of-tuneness at the same time. The trade-off is that there is no longer an integer number of pitch steps per octave so that this main pitch reference is sharp (1248 cents) or flat (1170 cents), but never exactly 2:1.
alpha = 78.0 cents/step = 15.385 steps/octave,
beta = 63.8 cents/step = 18.809 steps/octave,
gamma = 35.1 cents/step = 34.188 steps/octave.
Here is a comment about Beauty In The Beast (1986), from www.wendycarlos.com :"The title cut of the album, this compact piece whimsically blends two quasi grotesque ideas with a romantic theme in best "Ballet Russe" style. The new scales used for all of this are quite odd the first heard called Beta, splits the perfect fourth into two equal parts (actually eight equal steps of nearly 64 cents each ), the second, Alpha, does the same to the minor third (four equal steps for 78 cents each). While both scales have nearly perfect triads (two remarkable coincidences!), neither can build a standard diatonic scale, and so the melodic motion is strange and exotic. The two forces, beast and beauty, shift back and forth, and things are never quite what they seem."
Wendy (nee Walter) Carlos has been active in exploring experimental tunings. Of particular interest are her alpha, beta, and gamma scales. These split certain intervals into equal steps, which results in a strange sense of in-tuneness and out-of-tuneness at the same time. The trade-off is that there is no longer an integer number of pitch steps per octave so that this main pitch reference is sharp (1248 cents) or flat (1170 cents), but never exactly 2:1.
alpha = 78.0 cents/step = 15.385 steps/octave,
beta = 63.8 cents/step = 18.809 steps/octave,
gamma = 35.1 cents/step = 34.188 steps/octave.
Here is a comment about Beauty In The Beast (1986), from www.wendycarlos.com :"The title cut of the album, this compact piece whimsically blends two quasi grotesque ideas with a romantic theme in best "Ballet Russe" style. The new scales used for all of this are quite odd the first heard called Beta, splits the perfect fourth into two equal parts (actually eight equal steps of nearly 64 cents each ), the second, Alpha, does the same to the minor third (four equal steps for 78 cents each). While both scales have nearly perfect triads (two remarkable coincidences!), neither can build a standard diatonic scale, and so the melodic motion is strange and exotic. The two forces, beast and beauty, shift back and forth, and things are never quite what they seem."
Non-european cultures use several other micro-tonalities. A table of ten systems, plus reference units of pitch are compared to Equal Temperament on Wikipedia.

24 division notation
What about notating microtonality? Can this be achieved using conventional music notation?
While many experimental composers invent their own symbols for scoring music, a defacto system of symbols has come into use where modified accidentals are used to notate the pitch differences smaller than one semitone.
While many experimental composers invent their own symbols for scoring music, a defacto system of symbols has come into use where modified accidentals are used to notate the pitch differences smaller than one semitone.
This notation works best when the music is based on dividing the semitone by 2 or 4. It would need to be adapted to accommodate other alternative temperaments (such as 19 or 31 semitones per octave).
Sonic definitions
These terms are used to define speed in relation to sound. These are:
Subsonic - less than the speed of sound
Supersonic - greater than the speed of sound
Hypersonic - greater than 5x the speed of sound
Transonic - at or near the speed of sound
These are of interest to aviation and so on. For the audio engineer these three are of importance:
Sonic - audible to the human ear (ie 20Hz to 20KHz)
Infrasonic - below the lower frequency limit of human hearing (ie 20Hz)
Ultrasonic - above the upper frequency limit of human hearing (ie 20KHz)
Subsonic - less than the speed of sound
Supersonic - greater than the speed of sound
Hypersonic - greater than 5x the speed of sound
Transonic - at or near the speed of sound
These are of interest to aviation and so on. For the audio engineer these three are of importance:
Sonic - audible to the human ear (ie 20Hz to 20KHz)
Infrasonic - below the lower frequency limit of human hearing (ie 20Hz)
Ultrasonic - above the upper frequency limit of human hearing (ie 20KHz)
Reflected Sound Calculations
| reflected_sound_maths.pdf | |
| File Size: | 29 kb |
| File Type: | |
Speed of Sound - history
The speed of sound in air depends on the temperature, the humidity, and (to a lesser degree) the atmospheric pressure. No wonder it was not pinned down exactly until relatively recently.
| speed_of_sound-history.pdf | |
| File Size: | 60 kb |
| File Type: | |